The Engineering of Trust
Published on October 1, 2025
Creating a Secret in Public
I’ll admit it: I’m a cryptography snob. My password manager is a command center. I’d slap two-factor authentication on my coffee machine if I could. I guard private keys like nuclear launch codes. Yet I carried a professional shame: I trusted the little padlock icon. I preached Signal’s “end-to-end encryption” without understanding the mechanics behind it. I knew the what, not the how. For someone who lives by logic, “it’s magic” is never an answer.
We blindly entrust our most sensitive data to protocols most of us can't explain. What is the actual engineering chain that guarantees secrecy when anyone could be listening? When you peek under the hood, the reality is stranger, smarter, and far more elegant than any marketing slogan.
This is a deep dive into that chain. We’ll dissect the engines powering modern secure messaging, from the math that creates a secret in plain sight to the engineering that closes every loophole.
The Canonical Problem
Two parties, Alice and Bob, require private communication. Their only channel is insecure; an eavesdropper, Eve, sees everything. If Alice encrypts her message, how does she safely deliver the key? This is the canonical problem of cryptography: agree on a secret over a public channel.
The solution lies in one-way functions: operations that are easy to compute but computationally infeasible to reverse. A specific subset you may know are trapdoor functions, which are reversible only with a secret piece of information. The key exchanges we’ll dissect are even more pure, relying on one-way functions with no trapdoor.
The classic paint analogy illustrates this perfectly:
- Alice and Bob agree on a public color: Yellow.
- Alice secretly picks Red, mixes it with Yellow to get Orange, and sends it publicly.
- Bob secretly picks Blue, mixes it with Yellow to get Green, and sends it publicly.
- Alice mixes Green + her secret Red → Brown. Bob mixes Orange + his secret Blue → Brown.
Eve sees only the public mixes. She cannot deduce the secret components. They’ve established a shared secret in plain sight.
The First Engine: Diffie Hellman
Diffie Hellman was the first algorithm to turn this paint-mixing idea into a machine of numbers.
- The One-Way Function: Modular Exponentiation (
Result = base ^ exponent mod prime). Reversing this is the Discrete Logarithm Problem (DLP)—computationally intractable for large numbers.
Let's walk through the math with small numbers.
- Public Agreement: Alice and Bob agree on a prime
p = 23and a baseg = 5. Eve knows these.- Secret Keys:
- Alice secretly chooses
a = 4.- Bob secretly chooses
b = 3.- Public Exchange:
- Alice calculates
5^4 mod 23, which results in a remainder of 4. She sendsA = 4to Bob.- Bob calculates
5^3 mod 23, which results in a remainder of 10. He sendsB = 10to Alice.- The Shared Secret:
- Alice computes
10^4 mod 23, which results in a remainder of 18.- Bob computes
4^3 mod 23, which also results in a remainder of 18.
In real systems, these numbers scale to hundreds of digits, ensuring security. But the computational cost is high.
The Modern Engine: The Dance of Elliptic Curves
The demand for performance led us to Elliptic Curve Diffie-Hellman (ECDH). They offer equivalent security to Diffie-Hellman with drastically smaller keys, making them faster and more efficient.
The one-way function is Scalar Multiplication (k*P). Geometrically, this is visualized as "adding" a point P to itself k times along the curve according to specific rules.
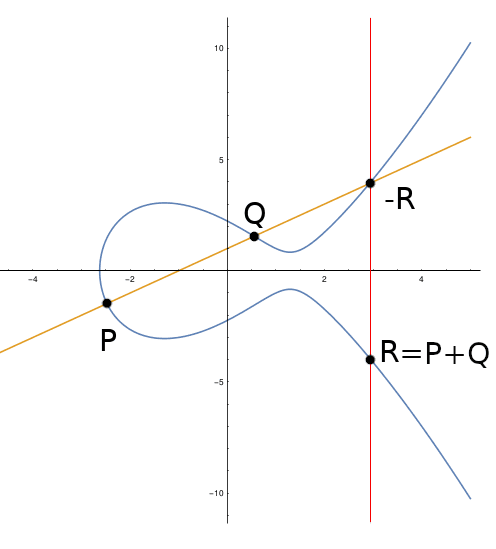
The geometric rule for "adding" points: a line through P and Q intersects the curve at a third point. The reflection of that point across the x-axis is R, the result of P + Q.
- To get 2* P: Draw a line perfectly tangent to the curve at point
P. This line will hit the curve at one other spot. Reflect that spot across the horizontal x-axis. That new point is2P. - To get 3*P: Draw a straight line from our original point
Pthrough our new point2P. That line will hit the curve somewhere else. Flip that point across the axis, and you have3P.
Given a starting point P and a final point Q, it's impossible to deduce k. That’s the Elliptic Curve Discrete Logarithm Problem (ECDLP). But how does a computer actually "draw tangent lines" to compute k*P? Let's get concrete. The most intuitive implementation is a classic algorithm called Double-and-Add. It translates the scalar k into a series of point doublings and point additions, directly analogous to its binary representation.
For a secret key k = 22 (binary 10110), the computer does the following:
- It scans the bits of
kfrom left to right. - For every bit, it performs a Point Double.
- Only when the bit is a '1', it also performs a Point Add.
The calculation for 22*P would unroll like this:
| Bit | Operation | Result |
|---|---|---|
| 1 | Double, then Add P | P |
| 0 | Double | 2P |
| 1 | Double, then Add P | 5P |
| 1 | Double, then Add P | 11P |
| 0 | Double | 22P |
This works beautifully. But that simple if bit == '1' check the very heart of the algorithm's logic is a catastrophic vulnerability. Mathematical elegance often introduces subtle, practical flaws.
The Ghost in the Machine: Side-Channel Attacks
The mathematics of ECDH are strong, but the hardware it runs on can leak secrets. This is where the physical world brutally intrudes on abstract math. An attacker doesn't need to break the ECDLP; they just need to listen to your processor.
The Double-and-Add algorithm has a fatal flaw: its execution path depends on the secret data.
- If a bit of your key is 0, the CPU performs one operation (Double).
- If a bit of your key is 1, the CPU performs two operations (Double and Add).
This difference, no matter how small, is a signal. An attacker can measure this signal to extract your key, bit by bit.
- Timing Attacks: A
Point Addtakes a few hundred extra nanoseconds. By precisely measuring the total time of the scalar multiplication over thousands of attempts, an attacker can statistically determine how many '1's are in your key. A more direct attack measures the time per loop: a short loop reveals a '0', a long loop reveals a '1'. One microsecond can leak everything. - Power Analysis: This is even more devastating. Different CPU instructions consume different amounts of power. By attaching an oscilloscope to the device's power line, an attacker can get a "power trace" of the computation. They can literally see the difference: a small power blip for a Double, and a larger, distinct power blip for a Double followed by an Add. The pattern of blips on their screen is a direct readout of your secret key.
The Hardened Engine: A Deep Dive into X25519 and the Montgomery Ladder
The solution is not stronger math, but smarter engineering: constant-time algorithms. The algorithm's operations must be completely independent of the secret data's value. The gold standard here is the Montgomery Ladder.
- The Mechanism: The genius of the Montgomery Ladder is its elimination of the data-dependent
ifbranch. Instead of one running total, it cleverly maintains two points,R0andR1. In every single loop iteration, it performs exactly one point addition and one point doubling, regardless of whether the secret key bit is a 0 or a 1.
At first glance, this looks like sleight of hand. How does doing a fixed dance of one add and one double per bit still give the right result, k*P? The answer is the ladder’s core invariant.
The Secret of the Montgomery Ladder: The Invariant
The algorithm preserves a single relationship across all iterations:
R1 – R0 = P
In every branch, the invariant survives. That invariant is what ties the operations back to correct scalar multiplication.
Let's look at its logic:
Initialize:
R0 = Point at Infinity
R1 = P
// Invariant: R1 - R0 = P - O = P
For each bit in the secret key k:
if bit == 0:
R1 = R0 + R1 // One Add
R0 = 2 * R0 // One Double
// Check invariant:
// (R0 + R1) - (2*R0) = R1 - R0 = P
else: // bit == 1
R0 = R0 + R1 // One Add
R1 = 2 * R1 // One Double
// Check invariant:
// (2*R1) - (R0 + R1) = R1 - R0 = PHow the Invariant Builds Scalar Multiplication
Track R0 as the bits of k are processed from left to right. After i bits, R0 equals kᵢ*P, where kᵢ is the integer represented by those i bits.
Example: k = 22 (binary 10110). Walk through the ladder:
Start: k = (empty), R0 = O = 0*P, R1 = P
| Bit | Before (R0, R1) | Operation | After (R0, R1) | R0 Value | Bits Processed |
|---|---|---|---|---|---|
| 1 | (O, P) | bit=1: R0=O+P, R1=2*P | (P, 2P) | P | 1 |
| 0 | (P, 2P) | bit=0: R1=P+2P, R0=2*P | (2P, 3P) | 2P | 10 |
| 1 | (2P, 3P) | bit=1: R0=2P+3P, R1=2*3P | (5P, 6P) | 5P | 101 |
| 1 | (5P, 6P) | bit=1: R0=5P+6P, R1=2*6P | (11P, 12P) | 11P | 1011 |
| 0 | (11P, 12P) | bit=0: R1=11P+12P, R0=2*11P | (22P, 23P) | 22P | 10110 |
Result: After processing all the bits of k, the register R0 holds the final result: 22P.
The workload is identical in both branches. The only difference is which register receives the result, a detail that is invisible to a power or timing attacker. The "long loop" vs "short loop" signal is gone. The power trace becomes a monotonous, repeating pattern, sealing the leak.
The Special Sauce for X25519
On a generic curve, the point addition R0+R1 and doubling 2*R0 are moderately expensive. Critically, to add two different points (x1, y1) and (x2, y2), you need all four coordinates.
However, on a Montgomery Curve, the specific operations used in the ladder (differential add and double) can be performed using only the x-coordinates of the points. You don’t need the y-coordinates at all during the loop. This makes the calculations drastically faster and simpler, requiring less code and fewer CPU cycles. The curve shape itself is purpose built to make its security algorithm, the Montgomery Ladder, run as fast as humanly possible.
This constant-time ladder is the core of X25519, but the protocol's hardened design goes even further, making it an opinionated system engineered from the lessons of past failures.
- No Input Validation: Unlike older curves that require slow, error-prone public-key validation, X25519’s math accepts any 32-byte input, neutralizing classical “Invalid Curve Attacks.” It computes a valid shared secret regardless of the input—but sloppy protocol use can still shoot you in the foot.
- Scalar Clamping: Before use, the secret scalar k is passed through a clamping function. This is a crucial, non-optional safety measure. It forces specific bits of the key into a known state (
k[0] &= 248; k[31] &= 127; k[31] |= 64). This mitigates a variety of sophisticated attacks, including small subgroup attacks, and ensures the Montgomery Ladder operates on a correctly formatted scalar.
X25519's design philosophy is to make the secure path the only path.
Beyond Secrecy: The Problem of Integrity
The handshake is done. We have a key. But here’s the catch: the beautiful, heavy mathematics of X25519 are for building bridges, not for moving traffic. They are brilliant for establishing a shared secret but far too slow to encrypt every single message. Imagine running that entire elliptic curve dance for every text you send—your phone's battery would die by lunch.
So, we use a hybrid approach. The heavy math (asymmetric) is run once to derive a lightweight, lightning-fast symmetric key. This key is then used with a symmetric cipher like AES to do the actual work of encrypting data.
This is where a new, more insidious class of attacks emerges. We've solved the secrecy problem, but we've created an integrity problem. Early encryption methods locked the box but failed to put a seal on it.
Let's look at a classic, now-deprecated mode called Cipher Block Chaining (CBC). The core problem it tries to solve is that if you encrypt the same block of data twice with the same key, you'll get the exact same encrypted block. This leaks information. Imagine an image where large areas are the same color; in an unchained mode, those would create visible, repeating patterns in the ciphertext.
CBC's solution is to chain the encryption of each block to the one before it. It does this using the XOR operation. To encrypt a block of plaintext, you first XOR it with the previous block of ciphertext.
Why XOR? Because it's a perfect, reversible "scrambler." XOR is a bitwise operation that acts like a toggle switch. If you XOR a value A with a key K, you get a scrambled result C. If you XOR C with the exact same key K again, you get your original value A back (A ⊕ K ⊕ K = A).
In CBC, the previous ciphertext block acts as that single-use, per-block "key." It scrambles the plaintext before it even enters the main encryption engine. This ensures that even if you have two identical plaintext blocks, P1 and P2, they will be XORed with two different ciphertext blocks (C0 and C1) before being encrypted. The inputs to the AES engine will be different, so the final outputs (C1 and C2) will also be completely different. It's a clever way to ensure no patterns are repeated, but as we'll see, this very mechanism is also its greatest weakness.
This very mechanism creates a fatal flaw, it makes the ciphertext malleable. An attacker can tamper with the encrypted message and produce predictable changes in the decrypted text all without ever knowing the key.
Let's stage the attack. You are sending an encrypted bank transfer instruction:
{"from":"Alice","to":"Eve","amount":"100"}
Eve intercepts the ciphertext. She can't read it, but she knows the format. She wants to change that "100" to "900". Here is the precise, devastatingly simple mechanic she uses:
Plaintext_Block[i] = Decrypt(Key, Ciphertext_Block[i]) ⊕ Ciphertext_Block[i-1]
The attacker cannot touch the Decrypt(Key, ...) part, that's protected by the secret key. But she has complete control over the previous ciphertext block Ciphertext_Block[i-1].
She knows that whatever change she makes to Ciphertext_Block[i-1] will be XORed directly against the output of the decryption, right before it becomes the final plaintext.
So, she crafts a Tampering Mask, she then modifies the ciphertext block that comes just before the block containing the amount:
Tampered_Ciphertext_Block[i-1] = Original_Ciphertext_Block[i-1] ⊕ Mask
When the receiver decrypts, this happens:
Final_Plaintext = Decrypt(Key, Ciphertext_Block[i]) ⊕ Tampered_Ciphertext_Block[i-1]
Final_Plaintext = Decrypt(...) ⊕ (Original_Ciphertext_Block[i-1] ⊕ Mask)
Final_Plaintext = (Decrypt(...) ⊕ Original_Ciphertext_Block[i-1]) ⊕ Mask
Final_Plaintext = Original_Plaintext ⊕ Mask
The result? The receiver's machine decrypts the message perfectly, without any errors. But the plaintext it sees is {"from":"Alice","to":"Eve","amount":"900"}. Integrity has been silently destroyed.
This is why modern systems use Authenticated Encryption with Associated Data (AEAD), with AES-GCM being the gold standard. AEAD provides a non-negotiable two-for-one deal: secrecy and integrity.
Here's how it neutralizes the attack. An AEAD cipher produces two outputs:
- The Ciphertext: The encrypted, unreadable data.
- An Authentication Tag: A small, fixed-size cryptographic checksum. Think of it as an unforgeable, tamper-evident seal.
If an attacker alters even a single bit of the ciphertext, the seal is broken. When the recipient tries to verify the tag against the tampered message, the check will fail, and the software will immediately discard the message. No more silent manipulations.
But how does this tag, this short string of bytes, guarantee the integrity of the entire message, from the first byte to the last?
It does this through cryptographic accumulation. The tag is not just a hash of the last block. It's the final state of a process that has sequentially mixed in every single block of the ciphertext.
Imagine a mixing bowl:
- The process starts with a secret value derived from the key, let's call it the Authentication Key
H.- The first block of ciphertext is thrown into the bowl and mixed with
H. The result is a new, scrambled value.- The second block of ciphertext is thrown into the bowl, which still contains the result from previous step. It's all mixed together again with
H.- This continues for every block. The state of the mixing bowl at any point is a function of everything that came before it. A change to the first block creates a different result in the next one, which then snowballs, causing every subsequent state to be completely different.
By the end, the value in the mixing bowl is a holistic representation of the entire, ordered sequence of ciphertext blocks. This final value is then encrypted one last time to produce the tag.
When the receiver gets the message, they perform the exact same mixing ritual on the ciphertext they received. If their final tag matches the one the sender sent, it is cryptographic proof that the message is authentic and has not been altered in any way.
With AEAD, the box is not only locked; it has a seal that is intrinsically tied to the exact contents of the box. Break the seal, and everyone knows. This is why modern secure messaging relies on AEAD: it protects both the secret and ensures it hasn’t been messed with along the way.
The Frontier: Forward Secrecy & Post-Compromise Security
Our system is secure. But what if a key is compromised years from now, could someone dig up old conversations and read them? That’s exactly the kind of problem the Double Ratchet Algorithm, pioneered by Signal, was built to solve. It keeps past messages safe and even lets the system recover after a compromise by rotating keys with every single message.
That’s a rabbit hole for another day I’ll cover it properly in a future post. But if you want to peek under the hood right now, the signal spec is the best place to start.
The Takeaway
We journeyed from paint-mixing metaphors to Diffie Hellman, evolved to the elegance of elliptic curves, hardened them with X25519, secured their output with AEAD, and glanced at the future with the Double Ratchet.
Each layer was forged in the fires of attack, failure, and ingenious engineering. Modern cryptography isn’t magic, it’s a living system, hardened by attack, refined by math, and engineered so we can forget it exists.